Т.Н. Прокофьева,
Е.А. Удалова

Построение модели отношений меньшей плотности.

В предыдущей статье (Геометрия интертипных отношений.Введение) мы познакомили читателей с геометрической моделью интертипных отношений, ввели понятия объема информационного метаболизма и характера наполнения информационных каналов как количественную и качественную характеристику обрабатываемой человеком информации. Напомним определения этих понятий:

Объем информационного метаболизма — количественная характеристика, соответствует количеству накопленной, усвоенной, перерабатываемой и транслируемой информации. В геометрической модели он представлен объемом куба.

Характер наполнения информационных каналов — качественная характеристика, соответствует положительно или отрицательно окрашенной информации, проходящей по информационным каналам.

Мы рассмотрели также плотные интертипные взаимодействия, представленные геометрически как стыковка кубов гранями — передача информации происходит одновременно по 4-м фукциям, составляющим грань куба:

• Дуальные — передача информации по верхней и нижней граням;

• Зеркальные — передача информации по правой и левой граням;

• Конфликт — передача информации по фронтальной и тыловой граням.

Итак, все грани куба заняты этими тремя отношениями, а общение с другими типами тем не менее происходит. Как же оно выглядит в геометрической модели?

Возьмем модель типа Дон Кихот, на которой мы решили рассматривать интертипные отношения. Пристроим к ней модели типов Дюма — сверху и Робеспьер — справа, как это делали в предыдущей статье (см. рис. 1). Образовавшееся в углу свободное место должен заполнить кубик типа, дуального для Робеспьера и одновременно зеркального для Дюма. Такой тип есть, это — Гюго. Таким образом, картинка замкнулась без противоречий, кубик типа Гюго вписался в оба отношения сразу. А с кубиком типа Дон Кихот он соприкасается по боковому верхнему ребру. Это отношения Активации.

Не имея одинаковых граней, кубики соприкасаются только ребрами. Можно предполагать, что общение в этом случае менее плотное, участвуют не 4, а только 2 функции одновременно.

Вспомним, что кубик Дюма может быть пристроен не только сверху, но и снизу, а Робеспьер, соответственно, не только справа, но и слева. Значит, для кубика Гюго есть еще три возможности расположения: вверху слева, внизу справа и внизу слева. Получается 4 варианта общения в отличие от плотных взаимодействий, в которых было только по два варианта.

Приходим к выводу, что отношения меньшей плотности обладают большей свободой. Кроме всего прочего, это означает и меньшую чувствительность к разнице в характерах наполнения информационных каналов, чем при плотных взаимодействиях.

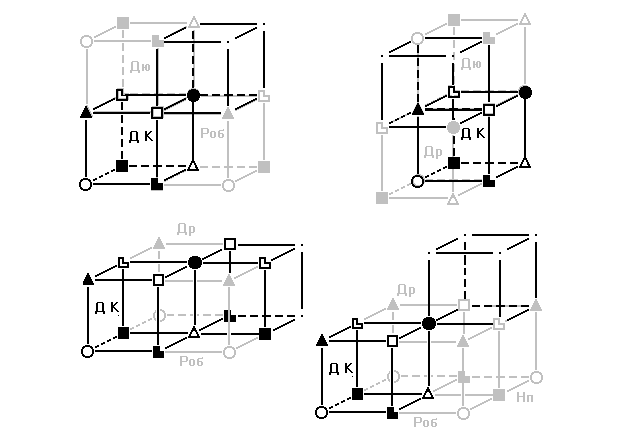
Рисунок A. Построение моделей отношений меньшей плотности:

Активация, Квазитождество, Суперэго, Погашение.

Аналогичным способом, базируясь на моделях типов Дюма и Драйзер, строим кубик типа, конфликтного для Дюма и одновременно дуального для Драйзера. Получаем тип Джек Лондон и модель отношений Квазитождества.

На моделях типов Робеспьер и Драйзер, строим кубик типа, конфликтного для Робеспьера и одновременно зеркального для Драйзера. Получаем тип Наполеон и модель отношений Суперэго.

Если теперь соединить вместе все построенные уже нами модели, то останется свободное место для кубика, соприкасающегося с кубиком Дон Кихота только в одной точке. Сюда по всем вышеизложенным правилам без противоречий вписывается кубик типа Бальзак. Таким образом получаем модель отношений Погашения, самых неплотных из всех рассмотренных.

Разберем теперь подробно каждое из отношений по той схеме, которая была принята в предыдущей статье.

Активация.

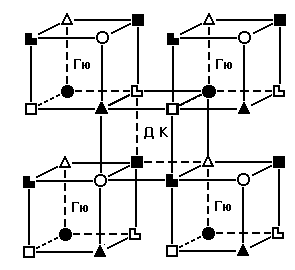
Рисунок B. Геометрическое представление отношений активации.

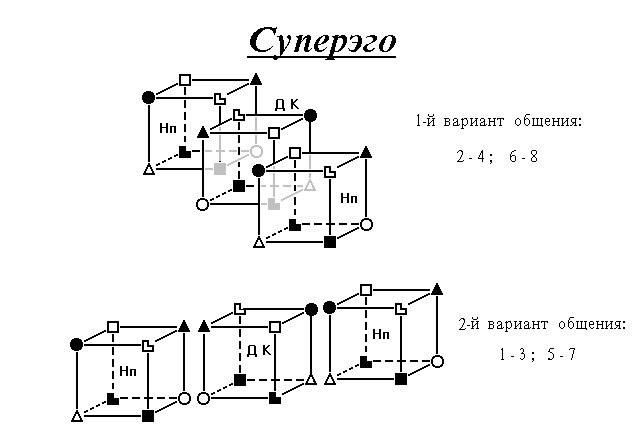
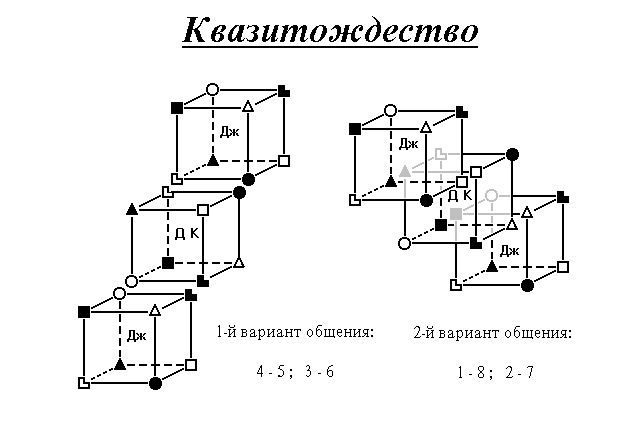
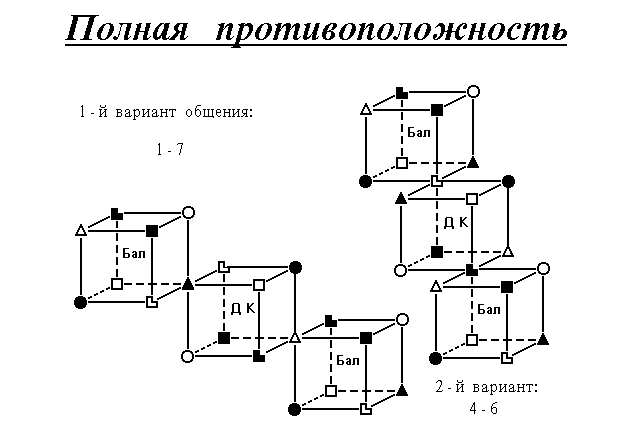
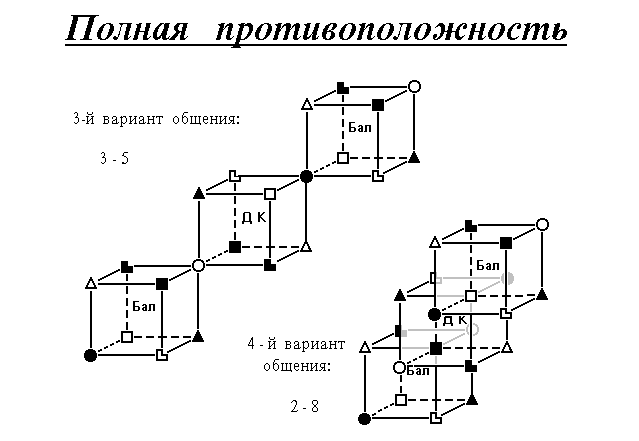
Рисунок E. Геометрическое представление отношений погашения.

Тождество.

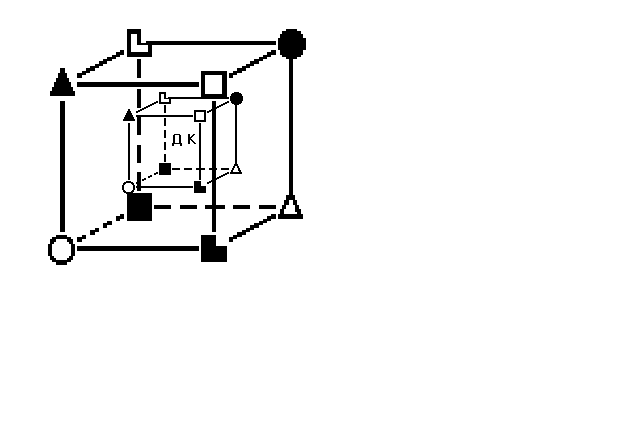
Предача информации осуществляется сразу по всем 8-ми функциям, обеспечивая полное взаимопонимание. Партнера как бы видишь изнутри, но это и утомляет.

О гибкости в данном случае говорить не приходится, т.к. нет других вариантов общения.

При разнице в объемах — учительство, обеспеченное прекрасным взаимопониманием, но, когда объемы выравниваются, партнер становится неразличимым, теряется интерес к нему.

Отношения тождества можно назвать сверхплотными: плодотворное общение может вытеснить из памяти все другие мысли и дела.

Отношения очень чувствительны к характеру наполнения информационных каналов, т.к. возможности диффузии огромны: сразу по 8-ми каналам.

Заключение.

Разобранные в первых двух статьях 8 интертипных отношений занимают все свободное пространство вокруг и внутри разбираемого кубика. А куда же поместить еще 8? Ведь все возможности контакта уже использованы, для других просто не осталось места. Может быть, в других отношениях уже нет контакта между одинаковыми функциями? Есть, и мы расскажем, как они выглядят в геометрическом представлении.

Продолжение темы:
Геометрия интертипных отношений. Применение