Осипов А.В.

Одним из ключевых свойств признаков Рейнина является их взаимозависимость, которая имеет эквивалентное математическое отражение в виде операции бинарного произведения. Для группы признаков, связанных такой операцией, удобно построить таблицу умножения [1]. Расстановка признаков в таблице при этом будет определяться порядком их расстановки по осям. В статье представлены таблицы умножения и порядок расстановки признаков к ним, а также рассмотрены способы применения таблиц на практике.

Ключевые слова: соционика, признаки Рейнина, взаимозависимость признаков Рейнина, таблица умножения признаков Рейнина, диагностика ТИМ.

Признаки Рейнина – один из ключевых элементов в фундаменте соционики, наряду с базисом Юнга и моделью А. Их знание и умение оперировать ими позволяет многократно повысить эффективность определения типа информационного метаболизма (ТИМ).

В данной статье представлены таблицы умножения признаков с порядком расстановки признаков к ним, представляющие собой инструментарий, который может быть использован непосредственно в работе соционика-диагноста; также рассмотрены некоторые практические ситуации, в которых они могут найти применение. Чтобы внести ясность в предмет и цели работы, необходимо будет сделать краткий экскурс в теорию признаков Рейнина.

В 1984 г. математик Г.Р. Рейнин рассмотрел приложение теории групп к соционике, представив социон как математическое множество S, состоящее из 16-и независимых элементов Т 1..Т 16 (типы информационного метаболизма). Результатом такого рассмотрения стал вывод о существовании 15 дихотомических признаков (или сечений), которым было присвоено имя Рейнина, и разработка на их основе теории малых групп [1].

В данной статье по возможности будут сохранены все обозначения и формулировки, введенные в [1]. Итак, несколько начальных определений.

Признаки Рейнина – это группа из 15 попарно ортогональных сечений социона S, включающая в себя 4 базовые дихотомии Юнга.

Чтобы полностью раскрыть это определение, необходимо ввести еще два – для понятий "сечение" и "ортогональные".

Для взятых выше в качестве примера признаков инвариантность к перестановке будет отражена наличием еще двух равенств в дополнение к уже имеющемуся:

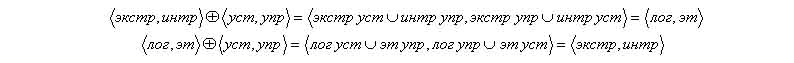
Соционическая интерпретация: первое равенство утверждает, что уступчивые экстраверты и упрямые интроверты - логики, а упрямые экстраверты и уступчивые интроверты – этики; второе – что уступчивые логики и упрямые этики - экстраверты, а упрямые логики и уступчивые этики - интроверты.

Взаимосвязь всех 15-и признаков Рейнина через операцию умножения удобно представить в виде таблицы умножения [1]. Расстановка элементов в такой таблице будет определяться порядком расстановки (фактически, нумерацией) признаков по осям, горизонтальной и вертикальной, и порядок этот, вообще говоря, может быть выбран совершенно произвольным образом. На данный момент практически используются два порядка расстановки: один был выбран из теоретических соображений Г.Р Рейниным, второй – из практических А. Аугустинавичюте.

В основу первого порядка расстановки были положены 4 признака Рейнина, составляющие базис Юнга:

Х₁=<экстраверсия, интроверсия>

Х₂=<логика, этика>

Х₃=<интуиция, сенсорика>

Х₄=<иррациональность, рациональность>

остальные 11 были введены путем их последовательного перемножения [1]:

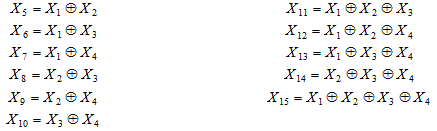
Пройдя определенный таким образом Г.Р. Рейниным путь самостоятельно, можно восстановить исходную нумерацию оставшихся признаков (в работах Рейнина она не указана, что лишает возможности воспользоваться такой таблицей на практике):

Таблица умножения для такого порядка расстановки признаков приведена в [1]:

Таблица умножения признаков Рейнина №1

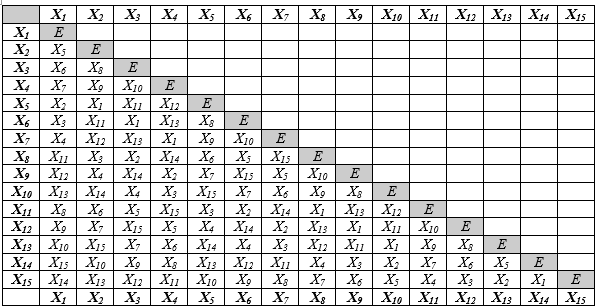
- таблица заполнена наполовину ввиду инвариантности операции бинарного умножения: X i * X j = X j * X i ;

- символ Е обозначает единичный оператор: E =< S , O > , где S – это весь социон, т.е. множество, содержащее все 16 элементов, O – пустое множество, т.е. множество, не содержащее ни одного элемента.

Второй порядок расстановки признаков представлен в широко известной и наиболее часто применяемой на практике таблице признаков Рейнина:

Нумерация признаков в таком порядке была выбрана для разбиения признаков на индивидуальные, диадные, квадровые. Вследствие смены нумерации, таблица умножения №1 недействительна, поэтому необходимо заполнить ее заново (поменять признаки в клетках местами) в соответствии с измененной нумерацией:

Таблица умножения признаков Рейнина №2

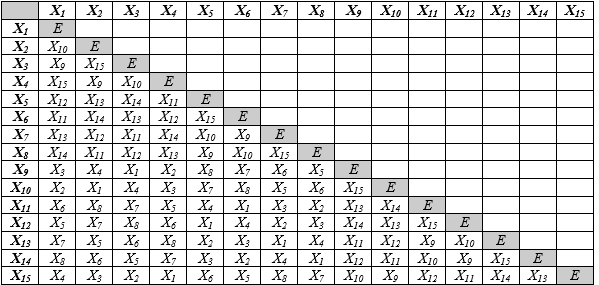
Опыт практического применения таблиц показал, что наиболее удобной является раскрытая таблица умножения признаков Рейнина, в которой используются не нумерованные символьные обозначения, а непосредственно сокращенные названия признаков (см. Раскрытая таблица умножения признаков Рейнина).

Итак, необходимый инструментарий для диагностики - таблицы умножения с указанием нумерацией признаков – представлен. В каких же ситуациях он может найти применение? Теория признаков Рейнина и практика их применения позволяют выделить следующие [2]:

1. Дополнительная проверка истинности определения двух признаков третьим.

Начальная ситуация: в процессе диагностики были определены 2 признака Рейнина – X i и X j, но остаются сомнения в правильности интерпретации.

Вопрос: как повысить достоверность определения признаков X i и X j?

Решение: по таблице умножения найти признак X k, являющийся взаимозависимым к ним, провести его независимую диагностику и сравнить с результатом бинарного умножения признаков X i и X j:

- если они совпадают ("="), то признаки X i и X j определены верно (либо оба неверно);

- если они не совпадают ("?"), то один из признаков X i или X jопределен неверно.

2. Определение труднодиагностируемого признака через два других (опосредованно)

Начальная ситуация: в процессе диагностики не удается однозначно интерпретировать признак X i.

Вопрос: можно ли определить X i не напрямую, опосредованно?

Решение: по таблице умножения найти признаки X j и X k (всего возможно 7 их разных комбинаций), являющихся взаимозависимыми к X i, провести их независимую диагностику и определить X i через операцию бинарного умножения X j и X k.

3. Проверка четверки признаков на достаточность для определения ТИМ

Возможность этой ситуации строится на еще одном свойстве признаков Рейнина [1]:

Любые 4 взаимно независимых признаков Рейнина являются базисом, достаточным для определения ТИМ.

Начальная ситуация: в процессе диагностики были определены 4 признака Рейнина: X i, X j, X k, X l.

Вопрос: является ли эта четверка базисом?

Решение: проверить все возможные тройки признаков: X i, X j, X k ; X i, X k, X l ; X j, X k, X l - на взаимозависимость по таблице умножений.

- если каждая из троек является независимой, то данная четверка признаков является базисом;

- если хотя бы одна из троек является взаимозависимой, то данная четверка признаков не является базисом.

Вообще говоря, для этой ситуации есть и другой способ решения, указанный Г.Р. Рейниным: искать эту четверку в списке из 840 возможных базисов. Но он представляется гораздо более трудоемким и потому менее эффективным.

Итак, подведем итог: в представленной статье подробно рассмотрено свойство взаимозависимости признаков Рейнина, представлены таблицы умножения признаков, обусловленные этим свойством, в символьной и раскрытой форме, а также рассмотрены способы применения таблиц на практике.

Следует отметить еще пару моментов, касающихся применения представленных таблиц. Во-первых, форма представления таблиц, раскрытая и символьная, естественным образом определяет область их применения: раскрытая более удобна при диагностике "вручную", символьная - при разработке компьютеризованных вариантов диагностики. Во-вторых, очевидно, что вышеуказанные способы – не единственные возможные, поэтому автор будет признателен любой информации, касающейся применения таблиц.

Автор выражает глубокую благодарность Т.Н. Прокофьевой и Г.Р. Рейнину за ценные советы и замечания по статье.

Список литературы

[1] Г.Р. Рейнин, «Соционика: Типология. Малые группы» - СПб: Изд-во «Образование-Культура», 2005

[2] Т.Н. Прокофьева, Методика диагностики типов информационного метаболизма. // Менеджмент и кадры, №2, 2004.

Раскрытая таблица умножения признаков Рейнина.

2008 г.